Besaran Menurut Arah dan Nilainya
Besaran Skalar
Besaran Skalar adalah besaran yang hanya memiliki nilai. Contoh besaran scalar adalah massa, panjang, waktu, energy, usaha, suhu, kelajuan, jarak, dan lain-lain.
Besaran Vektor
Besaran vektor adalah besaran yang memiliki nilai dan arah. Dalam ilmu Fisika, banyak besaran yang termasuk vektor, di antaranya perpindahan, gaya, kecepatan, percepatan, dan momentum.
Besaran Skalar
Besaran Skalar adalah besaran yang hanya memiliki nilai. Contoh besaran scalar adalah massa, panjang, waktu, energy, usaha, suhu, kelajuan, jarak, dan lain-lain.
Besaran Vektor
Besaran vektor adalah besaran yang memiliki nilai dan arah. Dalam ilmu Fisika, banyak besaran yang termasuk vektor, di antaranya perpindahan, gaya, kecepatan, percepatan, dan momentum.
Vektor dalam Cartesius
Untuk menggambarkan sebuah vektor di dalam diagram Cartesian maka dapat diskalakan sesuai dengan besaran magnitude yang dimiliki oleh vektor tersebut. Garis harus ditarik dari pangkal sampai garis tersebut mewakili besaran yang dimaksudkan dan pada bagian ujung diberi tanda panah. Misalnya V = 5 dengan arah 0° terhadap sumbu x, maka tampilannya pada gambar adalah sebagai berikut.
Jika vektor dinyatakan memiliki arah pada derajat tertentu, maka vektor digambarkan dengan memberikan sudut vektor terhadap sumbu x. Misalnya jika vektor V dinyatakan 45° terhadap sumbu x, maka tampilan gambarnya adalah sebagai berikut.

Perhatikan bahwa gambar vektor ini memiliki besaran nilai yang sama, tetapi memiliki arah yang berbeda.
Jika sebuah dua buah vektor memiliki besar dan arah yang sama maka vektor tersebut dapat dinyatakan sama. Misalnya vektor A pada gambar berikut ini, memilik nilai yang sama dengan vektor B. Perhatikan gambar.
Jika sebuah dua buah vektor memiliki besar dan arah yang sama maka vektor tersebut dapat dinyatakan sama. Misalnya vektor A pada gambar berikut ini, memilik nilai yang sama dengan vektor B. Perhatikan gambar.
Jika dua vektor tersebut berlawanan arah, tetapi tetap sejajar maka dapat dinyatakan secara matematis dengan memberikan tanda negative pada salah satu vektor.
Jika vektor B ternyata beberapa kali lebih besar dari vektor A maka secara matematis dapat digunakan perkalian vektor dengan u sebagai factor pengali.
Komponen Vektor
Sebuah vektor dapat merupakan penjumlahan dari dua
atau tiga komponen vektor, tergantung dari apakah vektor tersebut dalam
dua dimensi atau tiga dimensi. Komponen vektor dua dimensi adalah
komponen vektor terhadap sumbu x dan komponen vektor terhadap sumbu y.
misalkan sebuah vektor A, digambarkan seperti gambar berikut ini.
Komponen vektor terhadap sumbu x adalah Ax nilainya adalah A cos α.
Komponen vektor terhadap sumbu y adalah Ay nilainya adalah A sin α.
Untuk menjumlahkan beberapa vektor, maka haruslah terlebih dahulu diuraikan menjadi komponen-komponen vektor, setelah itu vektor sejajar dijumlahkan, lalu nilainya dicari. Misalkan vektor A dan B adalah dua vektor yang akan dijumlahkan maka nilai skalarnya dapat juga dinyatan sebagai berikut:
Operasi Matematika Vektor
Vektor dapat ditambahkan, dapat juga dikalikan, atau dibandingkan. Operasi perkalian atau penjumlahan vektor tentu tidak sama dengan operasi matematika pada besaran skalar lainnya.
Penjumlahan Vektor
Penjumlahan vektor hanya dapat dilakukan terhadap besaran besaran yang sejenis. Penjumlahan vektor dapat dilakukan secara grafis maupun menggunakan vektor komponen. Penjumlahan vektor secara grafis dapat dilakukan dengan metode jajargenjang dan metode poligon.
1. Metode Jajargenjang
Vektor A and vektor B merupakan vektor-vektor sejenis. Penjumlahan kedua vektor dengan metode jajargenjang dilakukan dengan membuat dua garis putus-putus yang masing-masing sejajar dengan vektor A dan B.
Penjumlahan vektor hanya dapat dilakukan terhadap besaran besaran yang sejenis. Penjumlahan vektor dapat dilakukan secara grafis maupun menggunakan vektor komponen. Penjumlahan vektor secara grafis dapat dilakukan dengan metode jajargenjang dan metode poligon.
1. Metode Jajargenjang
Vektor A and vektor B merupakan vektor-vektor sejenis. Penjumlahan kedua vektor dengan metode jajargenjang dilakukan dengan membuat dua garis putus-putus yang masing-masing sejajar dengan vektor A dan B.
Jika nilai vektor A dan vektor B diketahui serta sudut yang dibentuk oleh keduanya diketahui maka nilai resultan vektor R dapat diperoleh dengan menggunakan rumus cosinus, yaitu:
2. Metode Poligon
Penjumlahan beberapa vektor dengan metode poligon dilakukan dengan menggeser vektor kedua sehingga pangkal vektor kedua berimpit dengan ujung vektor pertama.
Penjumlahan dua vektor:
Penjumlahan tiga vektor:
3. Metode Vektor Komponen
Sekarang mari kita lihat bagaimana menggunakan metode vektor komponen untuk menjumlahkan vektor secara matematis. Anggap kita memiliki dua vektor, A dan B, yaitu:
Jika dijumlahkan maka resultannya adalah

Sementara itu, vektor R dapat dinyatakan dengan vektor satuan
Pengurangan Vektor
Pengurangan vektor adalah penjumlahan suatu vektor dengan vektor negatif. Jika vektor A dikurangi dengan vektor B maka sama dengan vektor A ditambahkan dengan negatif dari vektor B.
A – B = A + (-B)
Negatif dari vektor B yaitu vektor -B adalah suatu vektor yang memiliki nilai sama dengan vektor B namun berlawanan arah.
Pada gambar diberikan vektor A, B, dan C dan negatif dari ketiga vektor tersebut.
Dengan menggunakan vektor negatif, prosedur pengurangan vector secara prinsip sama dengan penambahan vektor. Berikut ini diperlihatkan hasil dari pengurangan vektor : A – B, B – C, B – A.
Jika vektor dapat dinyatakan dalam vektor-vektor komponennya, pengurangan vektor dapat dilakukan secara matematis. Misalnya:
A = Axi + AyjB = Bxi + Byj
Maka pengurangan vektor A dengan vektor B
A – B = ( Axi + Ayj ) – ( Bxi + Byj )= Axi – Bxi + Ayj - Byj
= ( Ax – Bx )i + (Ay - By )j
Perkalian Vektor
1. Perkalian Titik (dot product)
Dengan θ adalah sudut yang dibentuk oleh kedua vektor tersebut.
Jika vektor A dan vektor B dinyatakan dengan dalam vector satuan, maka perkalian titiknya diuraikan sebagai berikut
sedangkan hasil perkalian titik vektor A dengan dirinya sendiri, maka
Perkalian titik dapat digunakan untuk menentukan sudut yang dibentuk oleh kedua vektor, yaitu
2. Perkalian Silang
Beberapa sifat dari perkalian silang:
Source : https://marojahantampubolon.files.wordpress.com/2012/05/fisika-bab-i.pdf





















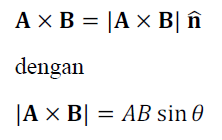









Lengkap pisun .....keren mbak uwi
BalasHapus